En los últimos años los agujeros negros están ganando cierta popularidad. Así lo indican las recientes detecciones de ondas gravitatorias, o la concesión de varios Premios Nobel en los últimos años a estos temas. Pero, ¿qué se sabe realmente sobre los agujeros negros? Es popularmente conocido aquello de que son regiones del espacio con una fuerza de atracción gravitatoria tan intensa que ni siquiera la luz podría escapar de ellos. Esto implica que, en la práctica, se observen como objetos invisibles u “oscuros” (de ahí el nombre). Esta propiedad es, efectivamente, muy notable, y quizás por ello los agujeros negros suelan despertar interés incluso en gente ajena a la física. Sin embargo, un aspecto tan o incluso más importante, y considerablemente más desconocido, es que aunque no podamos ver a los agujeros negros, sí que podemos realmente “escucharlos”. ¿Cuál es el sonido característico de los agujeros negros?
Para entender qué significa esto y poder responder a la pregunta, es ilustrativo repasar primero ciertas situaciones que nos sean más familiares. Por ejemplo, sabemos que al golpear un campana, una copa, una cuerda de guitarra, se produce un estado de vibración en el material en cuestión que es capaz de producir, a su vez, unas perturbaciones en las partículas del aire que se transmiten hasta nuestros oídos. Estas perturbaciones del aire son lo que conocemos como ondas sonoras, y son lo que identificamos como el sonido que hace la campana, la copa, o la cuerda. El sonido específico que nos llega depende del material que está vibrando. Así, si nos taparan los ojos sabríamos perfectamente distinguir, por nuestra propia experiencia, si el sonido que nos llega es de una campana o de una cuerda de guitarra. Además, cada objeto puede vibrar mediante un conjunto especial de modos (llamados “modos normales de vibración”) a unas frecuencias de oscilación concretas que son características del objeto en cuestión. El sonido que emite una campana al ser golpeada es una combinación de ondas sonoras producidas por estos modos normales de vibración. Estos modos característicos dependen intrínsecamente del material que está vibrando, por lo que el espectro asociado de frecuencias características puede utilizarse a modo de “código de barras” para saber identificarlos unívocamente. Si cambiamos el tamaño de la campana o la cuerda, la composición material de estos objetos, etc, las frecuencias características de vibración asociadas pueden cambiar también. Por tanto, si nos tapamos los ojos, no sólo sabríamos distinguir entre una cuerda de guitarra y una campana, sino entre diferentes cuerdas de guitarra o entre diferentes campanas.
Pues bien, de forma similar a una campana ordinaria, cuando un agujero negro es “perturbado“ respecto de su estado de equilibrio, por ejemplo cuando una partícula cae en su interior, la relatividad general predice que este objeto comienza a “vibrar” mediante un conjunto discreto de oscilaciones armónicas de frecuencias características. Se conocen como modos (quasi-)normales del agujero negro 1, véase la Fig. 1 para una ilustración. Sin embargo, hay una diferencia sustancial con el análogo musical: mientras una campana es un medio material susceptible de oscilar, el agujero negro está completamente vacío: es el estado final de una estrella que ha colapsado toda su materia a un punto de densidad infinita (para más detalles, véase el artículo “Agujeros negros, y un nobel de física matemático”). Pero si un agujero negro es simplemente el vacío más absoluto, ¿qué es lo que se supone que está vibrando? En contra de nuestra intuición newtoniana, estas vibraciones características son, sorprendentemente, oscilaciones del propio espacio-tiempo. Según la relatividad general, el espacio-tiempo es un ente dinámico, que reacciona y vibra cuando se le perturba, y la excitación de estos modos (quasi-)normales del agujero negro es un ejemplo muy ilustrativo de ello. Este es uno de los aspectos más distinguidos de la teoría de la relatividad general de Einstein acerca de la gravedad: ya no es que el espacio y el tiempo estén fusionados en el concepto de “espacio-tiempo” (algo que de por si puede volarnos la cabeza) sino que además éste puede evolucionar, oscilar o deformarse.
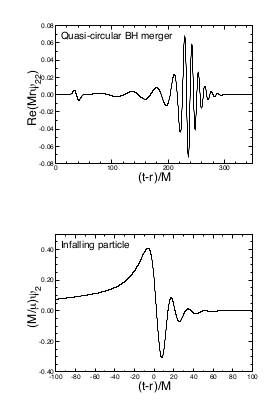
Las oscilaciones del espacio-tiempo se conocen como ondas gravitatorias, perturbaciones del espacio-tiempo que se excitan por algún suceso astrofísico (un colapso gravitatorio, una colisión con una estrella, etc serían el análogo al toque de campana) y que se propagan hacia el infinito. Estas ondas alcanzan la Tierra a su paso, y con ello alcanzan nuestros detectores, nuestros “oídos”. Al igual que ocurría con las campanas o cuerdas de guitarra, el espectro de frecuencias de estas ondas posee información muy valiosa sobre los parámetros del agujero negro, concretamente sobre su masa y su velocidad de rotación. Diferentes agujeros negros dan lugar a diferentes frecuencias características (diferentes sonidos que “oyen” nuestros detectores). Por tanto, la medida de estas frecuencias en observaciones de ondas gravitatorias permite estudiar la física subyacente del agujero negro con gran precisión. En particular, una situación de mucho interés es cuando dos agujeros negros colisionan y forman como resultado otro agujero negro. Como consecuencia de tal dramático proceso de formación, durante los primeros instantes el agujero negro final se encuentra perturbado y permanece en un estado de vibración transitorio. Dichas vibraciones u oscilaciones van atenuándose exponencialmente con el tiempo, al mismo tiempo que inducen una onda gravitatoria que se propaga hacia el infinito. Los interferómetros LIGO-Virgo (véase figura 2) son capaces de detectar las señales emitidas durante este proceso, y típicamente muestran la forma que se observa en la figura 3 2, conocida bajo el nombre de “waveform”.

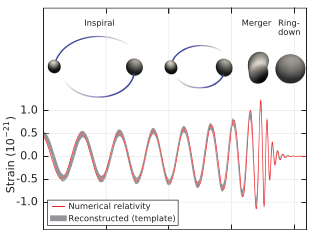
Esta última etapa en la colisión de dos agujeros negros se conoce como el “ringdown” (que traducido al castellano vendría a ser algo así como “decaimiento del sonido”). El análisis espectral y la determinación de las frecuencias características nos permite identificar al objeto resultante de la colisión, así como sus parámetros físicos (masa y estado de rotación).
Como hemos mencionado al principio, no podemos ver los agujeros negros porque no emiten luz (son invisibles), sino que sólo sabemos identificarlos por el “sonido gravitatorio” qué emiten. Pero, ¿pueden otros objetos estelares producir un sonido parecido? ¿y si el sonido que escucháramos en nuestros detectores no se correspondiera realmente con lo que teóricamente debería ser un agujero negro? Un ejemplo muy sencillo: ¿y si, esperando escuchar un “Stradivarius” en un concierto, lo que realmente escucháramos fuera el sonido de una copia barata de violín? En los últimos años 3, los físicos se han dado cuenta de que el sonido característico del “ringdown” podría ser realmente producido por cualquier objeto estelar oscuro que fuera suficientemente “compacto”, i.e. por una estrella cuyo cociente entre su masa y radio, 2M/R, fuera extremadamente cercano a 1 (para agujeros negros es exactamente 1). En relatividad general, objetos estelares estables tan compactos sólo podrían ser agujeros negros, pero si uno asume materia o escenarios más exóticos hay una gran variedad de objetos compactos que son capaces de “imitar” agujeros negros 4.
¿Podría ser que los eventos que han sido comunicados por los interferómetros LIGO-Virgo no se correspondieran realmente con la detección de un verdadero agujero negro? ¿Hay algún impostor? ¿Cómo podríamos distinguir unos objetos estelares de otros? Los agujeros negros son, por definición, objetos estelares con un horizonte. Dado que nada puede escapar de un horizonte de sucesos, esto significa que las ondas gravitatorias que “caigan” al horizonte permanecerán encerradas para siempre en el agujero negro. Sin embargo, esto no ocurre para una estrella ordinaria: al igual que las ondas sonoras son capaces de reflejarse en la superficie de una montaña y así formar una serie de réplicas del sonido emitido, las ondas gravitatorias que “caigan” a la estrella se reflejarán en su superficie y producirán una serie de “ecos” gravitatorios de la ráfaga inicial 5. Un ejemplo muy claro de lo que debería detectarse puede verse en la figura 4. La detección de estos ecos en las señales registradas por los interferómetros constituiría definitivamente una prueba directa de la existencia de nuevas estrellas. El descubrimiento de nuevos tipos de estrella abriría una nueva ventana de posibilidades en física, pues permitiría estudiar nuevos tipos de partículas, nuevas estados de la materia, etc. Y esto sería de mucha utilidad. Por ejemplo: ¿podría estar el enigmático origen de la materia oscura asociada a este tipo de estrellas exóticas?
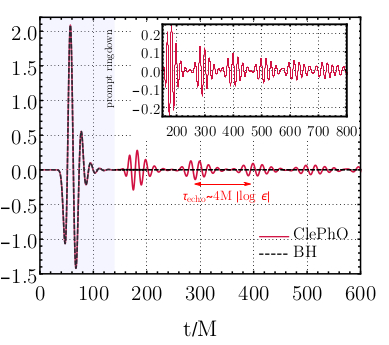
Pero la historia no acaba aquí: recientes estudios 6 han demostrado que la detección de ecos podría ayudar también a desvelar aspectos cuánticos de agujeros negros. En gravedad cuántica se espera que el área (energía) de un agujero negro sólo pueda tomar un conjunto discreto de valores. El carácter discreto del área implicaría, necesariamente, que un agujero negro cuántico no puede ser capaz de absorber realmente cualquier radiación gravitatoria: si la frecuencia de la radiación incidente es tal que el correspondiente crecimiento de área (energía) no se corresponde con uno de los valores permitidos, siguiendo las reglas de mecánica cuántica la probabilidad de absorción debe estar suprimida (esto es análogo a los niveles de energía de átomos y su interacción con radiación electromagnética). Como consecuencia, un horizonte cuántico debería ser capaz de dispersar ondas gravitatorias, i.e. de producir ecos, para unas frecuencias bien definidas. Lo interesante es que para ciertos modelos de gravedad cuántica estas frecuencias características resultan ser del orden del kHz, dentro de la ventana observable de los interferómetros LIGO/Virgo, por lo que su detección (o su no detección) proporciona información valiosa sobre la estructura cuántica del espacio-tiempo. Además, el espectro de frecuencias de los ecos es diferente al de cualquier estrella exótica (que tendría un espectro continuo), lo que permitiría distinguir experimentalmente entre ambos tipos de objetos.
A día de hoy, con la sensibilidad de los experimentos actuales y con los métodos de análisis de datos disponibles, no hay evidencia de estos ecos gravitatorios, por lo que no podemos afirmar nada todavía acerca de la existencia de estrellas compactas exóticas. No es de extrañar, sin embargo, pues sólo hace 5 años desde la primera detección de ondas gravitatorias. La astronomía de ondas gravitatorias se encuentra realmente en una fase bebé. El desarrollo y puesta en funcionamiento de interferómetros de siguiente generación planeados para las próximas décadas (como LISA o el Einstein Telescope) posibilitará alcanzar cotas de sensibilidad muy altas. Este desarrollo, junto con avances teóricos para el cálculo preciso y riguroso de las “waveforms”, permitirá dar respuesta a las preguntas planteadas. Sea como sea, la idea está clara: si queremos descubrir nueva física en el futuro, tendremos que escuchar atentamente a las estrellas.
Notas al pie:- K. D. Kokkotas and B. G. Schmidt, “Quasinormal modes of stars and black holes”, Living Rev. Rel. 2, 2 (1999); H.-P. Nollert, “Quasinormal modes: the characteristic sound of black holes and neutron stars”, Class. Quant. Grav. 16, R159 (1999).[↩]
- B. P. Abbott et al, “GWTC-1: A Gravitational-Wave Transient Catalog of Compact Binary Mergers Observed by LIGO and Virgo during the First and Second Observing Runs”, Phys. Rev. X 9 (2019) 031040.[↩]
- V. Cardoso, E. Franzin, and P. Pani, “Is the gravitational-wave ringdown a probe of the event horizon?”, Phys. Rev. Lett. 116 no. 17, (2016) 171101.[↩]
- V. Cardoso and P. Pani, “Testing the nature of dark compact objects: a status report”, Living Rev. Rel. 22 no. 1, (2019) 4.[↩]
- Véase de nuevo V. Cardoso, E. Franzin, and P. Pani, “Is the gravitational-wave ringdown a probe of the event horizon?”, Phys. Rev. Lett. 116 no. 17, (2016) 171101.[↩]
- I. Agullo, V. Cardoso, A. del Rio, M. Maggiore, and J. Pullin, “Potential Gravitational Wave Signatures of Quantum Gravity”, Phys. Rev. Lett. 126 no. 4, (2021) 041302.[↩]
