El pasado 6 de octubre se anunció que el Premio Nobel de Física de este año iba dedicado a la predicción teórica y observación astrofísica de agujeros negros. Concretamente, la mitad del premio fue otorgado al físico matemático Roger Penrose “por el descubrimiento de que la formación de agujeros negros es una predicción robusta de la teoría de relatividad general”, mientras que la otra mitad del premio fue galardonada a los astrofísicos Andrea Ghez y Reinhard Genzel “por el descubrimiento de un objeto compacto supermasivo en el centro de nuestra galaxia”.
La noticia del premio a este tema es doblemente remarcable. En primer lugar, porque históricamente el paradigma de agujero negro fue considerado durante muchas décadas un tema especulativo y marginal en la comunidad científica: no fue hasta los años 60 y 70, con las observaciones de quasares 1 y de fuentes de rayos X, que el tema de agujeros negros se convirtió en “mainstream” en física. Y en segundo lugar, porque parte del premio ha decidido otorgarse a un resultado teórico con un fuerte componente matemático, el obtenido por el físico matemático Roger Penrose. No es habitual que la Real Academia Sueca de las Ciencias decida otorgar parte de un Nobel de Física a una predicción tan teórica, pues, como resulta lógico, un premio de tal calibre sólo debe otorgarse a un determinado tema si realmente existe evidencia científica muy contundente de su realidad física. Intentemos ver aquí por qué el artículo premiado de Penrose [1] llega a esos niveles de excelencia.

En primer lugar: ¿qué es un agujero negro? En palabras sencillas, un agujero negro es simplemente una región del espacio donde la atracción gravitatoria es tan intensa que, una vez dentro, ni siquiera los rayos de luz serían capaces de escapar. Dado que no hay nada que sea capaz de propagarse a una velocidad mayor que la velocidad de la luz, eso significa que toda ‘información’ que penetre dentro de dicha región quedará perdida para siempre. Esta es la predicción de la teoría de la relatividad general, la teoría más precisa y simple que tenemos para describir todos los fenómenos gravitatorios en el universo. Debido a esta propiedad, el borde que delimita la región de agujero negro se conoce como ‘horizonte de sucesos’. La siguiente pregunta es obligada: ¿por qué son los agujeros negros (u horizontes) objetos de interés físico? Básicamente, porque a día de hoy sabemos que los agujeros negros se producen, principalmente, como resultado de la “muerte” de una estrella muy masiva. Podemos entender las estrellas como distribuciones aproximadamente esféricas de materia, constituidas mayoritariamente de gas hidrógeno. Las estrellas permanecen en equilibrio durante la mayor parte de su existencia: la presión interna originada como consecuencia de una serie de reacciones nucleares del hidrógeno compensa la fuerza gravitatoria que ejerce el propio peso de la estrella, y evita que la estrella ‘colapse’ a un punto. Sin embargo, una vez se acaba el “combustible” nuclear en el interior de la estrella, dicha presión interna desaparece. Como consecuencia, si la masa de la estrella es suficientemente grande 2, una vez se acabe el hidrógeno sabemos que no existe ninguna otra fuerza interna lo suficientemente potente como para evitar el colapso, haciendo que toda la masa de la estrella se reduzca a un punto de densidad infinita (una ‘singularidad’), generando como resultado un campo gravitatorio tan intenso capaz de definir un horizonte: “ha nacido una (nueva) estrella”, como dirían en Hollywood. O más bien, un agujero negro.
A pesar de que actualmente tenemos una interpretación clara de estos objetos y de su proceso de formación, costó realmente muchas décadas entender lo que significaban las soluciones de las ecuaciones de Einstein que los describían, pues en aquella época los científicos no comprendían totalmente la fuerte relación entre geometría y física que subyace a la relatividad general. De hecho, no fue sino este entendimiento lo que popularizó a estos objetos como ‘agujeros negros’ a partir de 1967. Es por eso que para entender la importancia del artículo de Penrose de 1965 premiado [1] hay que situarse en el contexto histórico adecuado, donde la concepción de agujero negro era todavía, digamos, difusa. En aquellos años las observaciones en astrofísica indicaban la existencia de objetos estelares en el universo que emitían una cantidad ingente de energía en forma de radiación electromagnética (luz), nunca antes observada en estrellas. Fueron resultados experimentales muy importantes en tanto que desconcertaban a los físicos de la época, pues no se conocía ningún mecanismo en física nuclear que fuera capaz de producir tales cantidades de energía en el interior de una estrella. Estas observaciones en astrofísica revivieron entonces el interés sobre las cuestiones de colapsos estelares; cuestiones que habían sido propuestas hacía más de 30 años antes, iniciadas por Chandrasekhar a principio de los 30 [2], y rematadas en 1939 cuando Oppenheimer y Snyder [3] publicaron su ahora célebre artículo sobre formación de agujeros negros a partir del colapso de estrellas perfectamente esféricas. Durante esos años se pensaba que el colapso estelar total era un fenómeno físicamente “absurdo” 3, por lo que dichos resultados no fueron muy apreciados en astrofísica 4. Sin embargo, las circunstancias obligaban a tener una mentalidad más abierta, y se empezó a conjeturar ahora sobre la posibilidad de que dichas emisiones altamente energéticas observadas recientemente por los astrofísicos pudieran realmente tener alguna relación con el proceso de colapso de estrellas.
El colapso gravitatorio de Oppenheimer-Snyder presentaba un problema. El modelo predecía la posibilidad de que no existiese un estado de equilibrio final para una estrella: ésta se contrae, haciéndose progresivamente más pequeña, hasta que toda su masa se concentra en un punto del espacio “singular” de densidad infinita. La existencia de esta singularidad presentaba un problema conceptual serio, pues es físicamente absurda, y ello deslegitimaba el modelo. El que toda la estrella acabara en un punto “singular” era consecuencia directa del colapso gravitatorio infinito, y por ello la posibilidad real de que existieran “estrellas completamente colapsadas” (como se llamaban a los agujeros negros en aquella época) inquietaba demasiado a los físicos. Hasta el punto que se argumentó [5] que la aparición de esas singularidades era una simple consecuencia de la sobre-simplificación del modelo de Oppenheimer-Snyder, pues al fin y al cabo este resultado asumía que la estrella era perfectamente esférica. ¿Acaso este modelo era demasiado simplista? En astrofísica las estrellas siempre tienen algo de rotación, la cual rompe la simetría esférica, por lo que durante un tiempo se pensaba que dicha singularidad, y por consiguiente el colapso gravitatorio en sí mismo, era realmente un resultado matemático artificial, y que se evitaría como consecuencia del efecto de rotación en sí o de otros efectos derivados de la ruptura de simetrías (distribución de materia no uniformemente distribuida, etc).
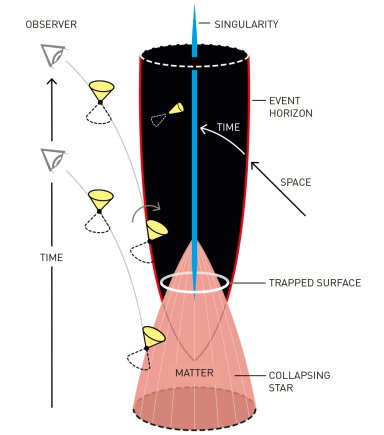
Para saber si esas conjeturas eran ciertas, había que resolver las ecuaciones de Einstein (las cuales describen todo fenómeno dinámico asociado a gravitación) para modelos estelares más realistas, sin hipótesis de simetrías. Surgía entonces una complicación: dichas ecuaciones son tremendamente complicadas y encontrar una solución exacta suya era realmente una tarea hercúlea; en aquellos años además ni existía la tecnología ni el formalismo teórico actual necesarios para extraer soluciones mediante un ordenador.Es aquí donde Penrose entra en juego [1]. Penrose se propuso resolver esta cuestión sin llegar a resolver explícitamente las ecuaciones de Einstein, sino estudiando en su lugar el comportamiento de las trayectorias de partículas en un espacio-tiempo genérico. Para caracterizar el surgimiento o no de singularidades, introdujo la noción de “incompletitud de geodésicas”: si las trayectorias que siguen las partículas de la estrella en el espacio-tiempo llegan a un “punto muerto”, y no pueden extenderse más allá, eso indica la aparición de singularidades. Un ejemplo sencillo a visualizar de una singularidad es la punta de un cono ordinario 5: las curvas de la superficie del cono que acaben en la punta no pueden “extenderse” más allá. La conclusión a la que llegó Penrose fue que, si se asumía que las ecuaciones de Einstein eran válidas, la formación de singularidades era algo bastante común en relatividad general (esto es lo que se conoce en la literatura como el Teorema de Singularidad de Penrose). En otras palabras, que el modelo de Oppenheimer-Snyder, a pesar de las simplificaciones matemáticas, era esencialmente correcto. La relevancia histórica de este artículo es altísima, no sólo porque Penrose precisó la idea de “incompletitud geodésica” para demostrar la existencia de singularidades, sino porque además introdujo por primera vez la noción de “superficies cerradas atrapadas” (closed trapped surfaces, en inglés), una contribución fundamental para entender realmente la noción del horizonte de los agujeros negros. Además de la validez de las ecuaciones de Einstein, la formación de una superficie cerrada atrapada era la condición necesaria que Penrose encontró para la aparición de singularidades: si siguiendo la trayectoria de una partícula se forma una superficie atrapada, entonces es imposible, en relatividad general, evitar el colapso gravitatorio de la estrella hacia una singularidad.
Con el Teorema de Singularidad de Penrose, la cuestión teórica de si en Relatividad General los agujeros negros (“estrellas completamente colapsadas”) podían originarse como resultado de un colapso gravitatorio de una estrella quedó completamente resuelta. La formación de agujeros negros es, efectivamente, una predicción rigurosa y robusta de la relatividad general. La siguiente cuestión era buscar evidencia de que los agujeros negros realmente existiesen en nuestra realidad física, y comprobar así la validez de la teoría de Einstein. A día de hoy los astrofísicos nos indican con gran seguridad la existencia de objetos muy masivos, muy compactos , y totalmente oscuros en el universo, como por ejemplo el objeto situado en el centro de nuestra galaxia (observaciones [6, 7] premiadas, recordemos, con la segunda mitad del Nobel de Física de este año). Por otro lado, hay teoremas en relatividad general que nos garantizan que, bajo ciertas suposiciones físicamente razonables, el único objeto compatible con dichas observaciones es un agujero negro. Por tanto, o bien existen los agujeros negros, o bien la relatividad general es insuficiente / fracasa en sus predicciones. Cualquiera de las dos opciones es merecedora de un nobel de física, c.q.d.
Referencias:
[1] R. Penrose, “Gravitational Collapse and space-time singularities“, Phys. Rev. Lett. 14, 57 (1965).
[2] S. Chandrasekhar “The Maximum Mass of Ideal White Dwarf Stars”. Astrophysical Journal. 74: 81–82. (1931).
[3] J. R. Oppenheimer, H. Snyder, “On continued gravitational contraction”, Phys. Rev. 56, 455, (1939)
[4] A. Einstein, “On a stationary system with spherical symmetry consisting of many gravitating masses” Ann Math XI, 922 (1939)
[5] E. M. Lifshitz, I. M. Khalatnikov “Investigations in relativistic cosmology”, Advances in Physics, vol. 12, no. 46. pp. 185–249 (1963)
[6] Eckart, A. and Genzel, R., 1996, “Observations of stellar proper motions near the Galactic Centre”, Nature, vol. 383, no. 6599. pp. 415–417.
[7] Ghez, A. M., Klein, B. L., Morris, M., and Becklin, E. E., 1998, “High proper-motion stars in the vicinity of Sagittarius A*: Evidence for a supermassive black hole at the center of our galaxy”, The Astrophysical Journal, vol. 509, no. 2. pp. 678–686.
Notas al pie:- Los quasares son objetos muy compactos observados en el cosmos que emiten una luminosidad 1012 veces la del Sol y localizados a distancias enormes (“cosmológicas”).[↩]
- Si la masa de la estrella no es tan grande, cuando el hidrógeno se acaba es posible la formación de “estrellas de electrones” (conocidas como enanas blancas) o estrellas de neutrones, donde la fuerza gravitatoria es compensada por una fuerza interna de origen cuántico.[↩]
- Es notorio el episodio entre Chandrasekhar (por aquel entonces estudiante) y Eddington (quizás el astrofísico más influyente de la época) en una conferencia de la Royal Astronomical Society de 1935. Sobre los resultados de Chandrasekhar, se dice que Eddington afirmó: “Various accidents may intervene to save the star. But I want more protection than that. I think there should be a law of Nature to prevent the star from behaving in this absurd way!” hasta el punto de llegar a ridiculizarlos públicamente calificándolo de “bufonería estelar”. Por otro lado, el propio Einstein publicó un artículo, [4], poco antes de [3], concluyendo que el colapso gravitatorio total tenía que ser imposible.[↩]
- Hubo factores no científicos que seguramente contribuyeron a que este artículo no tuviera más impacto del que debería haber tenido. Como por ejemplo, que fuera publicado exactamente el mismo día en que Alemania invadiera Polonia, y se iniciara formalmente la II guerra mundial. También coincidió con el día en que Bohr y Wheeler publicaron su artículo sobre el mecanismo de fisión nuclear; dadas las circunstancias de la época resulta natural pensar que ensombreciera al artículo del colapso gravitatorio.[↩]
- Técnicamente este tipo de singularidad no es del mismo tipo que las singularidades de curvatura en relatividad general, pero sírvase de ilustración.[↩]

2 opiniones en “Agujeros negros y un Nobel de Física “matemático””